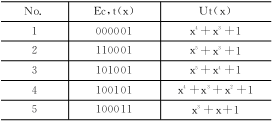
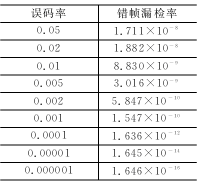
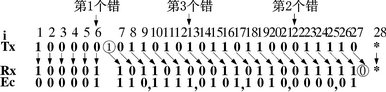
When data is erroneously transmitted and the error frame is missed, it means that the erroneous data is sent to the application layer. Unless the application layer has additional data identification measures, this data may cause unpredictable results. The CAN protocol claims to have a very low false frame miss detection rate (4.7×10-11×error rate) [1]. Some promotional materials are released under certain conditions for 1000 years before they are missed. This is incorrect. . The error rate of missed frame is a very important indicator. Many applications use CAN when they see the instructions on the Bosch CAN2.0 specification. However, there is very little public information on the source of this indicator [2], and there is very little discussion [3], which makes it difficult for users to confirm or verify it, which brings risks to users. In this paper, we use the method of reconstructing the error detection example, and derive the lower limit of the missed error detection frame of CAN, which is several orders of magnitude larger than that claimed by CAN. In many applications, CAN is the choice of reliability and price balance, or has been produced and used for a long time. In the face of this newly discovered problem, there is an urgent need for a “patches†before the CAN itself is improved. To improve. Due to the limited space, we can only summarize the derivation process of the missed frame error rate, focusing on providing solutions. This article refers to the address: http:// 1 Discussion on the literature of CAN miss detection error frame probability The Bosch CAN 2.0 specification [1] states that its missed error detection frame probability is less than the message error rate × 4.7 × 10-11. Its source is found in reference [2], which does not provide an analysis algorithm that produces missed detection, only the formula is obtained with a large number of simulations. To determine whether a frame will be missed after an error, at least 2 times of CRC calculation is required. For each bit, only several instructions are required for the assembly language. The frame of 80 to 90 bits considered in this paper, the CRC covers 58 to 66 bits. It is necessary to cycle 58 to 66 times. For the PDP11 or VAX machine commonly used in 1989, a machine instruction should be about 0.1 μs, and the judgment of one frame should be 0.07 ms. Even if it is not stopped for one year, it can be 2.20×1011 frames. 58 bits can form 258=2.88×1017 different frames, plus 58×57 different combinations of positions with 2-bit bit errors, so the simulation that can be done is only a small part of the possible situation (one millionth ). Since the sample is too small, it is difficult to conclude the influencing factors for the inductive formula. In 1999, Tran[3] also studied the missed frame miss rate. In view of the difficulty of analysis, he also used a large number of computer simulation methods. For 11-bit ID and 8-byte data frames, he used a 600 MB Alpha server. . As discussed above, although the amount of simulation is large, it is still a very small part of the possible situation. Another standard CANopen Draft Standard 304 (2005) related to CAN has a false frame miss detection rate of (7.2 × 10-9) [4]. The same data from the CAN Automation Association is unmatched. 2 The export of missed rate of new error frame The research method in this paper is to construct an instance of missed detection, determine the probability that the instance takes up the possible frame, multiply the probability of multi-dislocation corresponding to the instance, and then find all possible instances to get the wrong frame of CAN. Missed detection rate. This paper analyzes the two dislocations that are most likely to cause missed detection and then expands to have multiple dislocations. The data field takes 8 bytes and assumes that errors occur in the data field. It does not take into account the scattered multi-bit error detection rate when the CRC check capability is exceeded, so the lower bound of the error detection error frame probability is obtained. 2.1 When there is an error in the CAN bit filling, the bit order is staggered. When there is a bit error in the bit stream that may cause padding, it may cause the sender and the receiver to execute the padding rule only, causing confusion of the padding bit and the information bit. An error occurs in the third bit transfer of Fig. 1(a). As a result, the padding bit 1 of the sender is misinterpreted as data 1 by the receiver, and the entire received data is one bit longer than the transmitted data. The error in the third bit transfer of Fig. 1(b) causes the receiver to generate a condition for deleting the padding bit, so it deletes the transmitted data 1 and the received data stream is one bit shorter. Figure 1 CAN bit filling rule makes the received bit stream change after an error It can be known from the bit stream change that if the 2 bit errors that occur are exactly the type of Figure 1(a) and the type of Figure 1(b), the length of the transmitted data stream and the received data stream will still be equal. Both errors occur in the data field, and other tests by CAN cannot find them. 2.2 Conditions for missed detection The transmitted bit stream and the received bit stream can be written in polynomial forms Tx(x) and Rx(x). The CRC check divides the two expressions by the CAN generator polynomial G(x), and the resulting remainder is called the CRC value. If the two remainders are the same, the CRC test passes. When a transmission error occurs, Rx (x) = Tx(x) + U(x) × G(x), the remainder obtained for Tx(x) and Rx(x) is the same, and an error occurs. Missing detection of the frame. So as long as U(x) is found, an instance of missed detection can be constructed. 2.3 Determine the fault polynomial U(x) from the tail of Ec(x) In order to make the reader understand the rationality of the derivation process, the following are examples. After the error of Figure 1(b) has occurred before, the i bit of Tx is received as the i-1th bit by Rx. The error occurring in the tail corresponds to the case of Fig. 1(a) as shown in Fig. 2. In the figure, these 6 bits of Tx constitute the tail of the missed detection instance, and the first bit 1 is used to isolate the influence of the previous bit value, so that the padding bit must be generated after the last 5 bits. Due to a fault in the transmission, Rx no longer has 5 consecutive 0s. The padding bits of Tx are treated as data bits by Rx, and Rx and Tx are aligned, and there is no longer a bit error in subsequent transfers. The Rx is also different depending on the position where the bit error occurs, and the error sequence Ec is also different. This Ec is also the tail of the entire error sequence, denoted by Ec,t. As can be seen from Figure 2, there are 5 different error sequence tails. Obviously, inverting 0/1 in Tx does not change the form of the tail Ec,t of the error sequence. Figure 2 The second transmission error causes the padding bits to be misinterpreted as information bits. After the error sequence tail form Ec,t is known, the error-error polynomial tail Ut that satisfies it can be found. Express the coefficients of each polynomial as: To satisfy the tail of Ec, t=G×Ut, the coefficients have the following relationship: In fact, Ec, t, G are all arranged in reverse order: Similar to the method of finding the CRC value, the inverse coefficient of Ut can be obtained by dividing Ec, tR×x5 by GR, and Ut is obtained. The coefficient (1100, 0101, 1001, 1001) and the Ec, t coefficient of the polynomial G generated by CAN obtain the error-error polynomial Ut satisfying the tail form of the error sequence, as listed in Table 1. Table 1 Error sequence tail form and missed error polynomial Ut(x) 2.4 Ut expansion forms the Ec header Adding an item above x5 to Ut becomes U, which does not affect the form of the Ec tail, but it increases the length of the error sequence. The Ec and Tx sequences generated by this U will also be missed. The collection of Tx in different locations within the data domain constitutes all missed instances. After the first bit error occurs, the Tx-Rx bit order is not immediately started, and there is a bit error when there is a padding bit. 2.5 Construction Error Instance Tx Taking Ut=x4+x3+1 as an example, a transmission error occurs at the first bit of the corresponding tail, and U=x6+x4+x3+1 after Ut plus x6, and Ec=U×G=(1110,1111) is calculated. , 0101, 1010,0000, 01), the length of the entire error sequence is 22 bits. The Ec determines that the position of the first transmission error in the header is 6, and if it is assumed to be a missed padding dislocation, the information dislocation at the tail should be taken. Assume that Tx is sent to 100000 in the head, R1 is received at the 6th bit, and the first bit is wrong. The 7th bit Rx gets padding 1 and is not deleted. The 7th bit of Tx can be Ec. And Rx finds 0, and then pushes back bit by bit to get an example of Tx occurrence of miss detection, as shown in Figure 3. Figure 3 is a Tx instance constructed with a leak detection error. The length of the Tx sequence in this example is 27 bits. There are 227 types of Tx of this length, each of which may be wrong, but the reconstructed one will miss the detection when 2 bit errors occur in a particular bit. When this Tx has a bit error at another location, it will be able to check for errors, so it is a suspicious instance that may be missed. There are 4 possibilities for the Tx header: Tx=10000(0), 10000(1), 01111(1), 01111(0). (The bits in parentheses are wrong in the transmission). Therefore, these suspicious instances account for 2-25 of possible Tx. Suspicious Tx will have 64-27+1=38 locations in the 64 bit data field. For the headers Tx=100000 and 10001, the upper 4 bits can coincide with the DLC of the CAN. For Tx=011111 and 011110, the highest bit can coincide with DLC0, so this Tx instance appears in the frame of the 8-byte data field. The possible number is 39. Thus, this type of missed detection has a probability of 39×2-25=1.16×10-6. When the bit error rate is 0.02, the probability of 2 bit errors in 64 bits is (1-0.02) 62 × 0.022 = 1.14 × 10-4. The missed rate of CAN error frame caused by this example is 1.32 × 10 -10, already larger than Bosch's indicator. Considering that x can be increased in U, k can be from 6 up to 43, and various xk terms have 237=1.37×1011 combinations. It is necessary to calculate each U, although their probability of missed detection is different, the increment is still very big. Also consider the contribution of different Ut, it can be seen that the CAN miss frame miss rate is very large. 2.6 Calculation results According to the above analysis, the program pcan.m running in MATLAB is compiled. Format winter e format is set in MATLAB, and pcan(ber) can be run to get the results of different bit error rate ber, as listed in Table 2. Table 2 Typical CAN Leak Detection Error Frame Probability The missed frame miss rate of ber=0.02 in the table is 1.882×10-8, and the missed detection rate given by reference [2] at the same bit error rate is: low speed system 4.7×10-14 and high speed system 8.5× 10-14. It can be seen that the difference is great. For a 500 kbps system, assuming a bus utilization of 40% and a frame length of 135 bits, the CAN system will issue a missed error frame at 9.96 hours. 3 ways to improve the missed frame miss rate As can be seen in the analysis of this paper, since the padding rule requires synchronous transmission and reception, the CRC check will be greatly disturbed when the synchronization is not performed. For example, the CRC check can detect all the odd errors, and the multi-bit is less than 5 bits. Errors can be detected, but as long as there are pairs of filled dislocations, the increased odd errors can also be missed, and the increased multi-bit errors can also be missed, as shown in Figure 4. Figure 4 shows an example of multiple dislocations The root cause of the miss detection is that the CAN CRC is generated before the padding rule is executed. The most fundamental solution is to place the CRC check after the padding rule is executed, as pointed out in [3]. However, this will fundamentally modify the CAN protocol, and how to improve the compatibility before and after the application has been a large number of applications is a difficult task. As a partial correction, reference [3] suggests adding additional tests. When adding a new different CRC test in the data field, according to the analysis method of this paper, when the error polynomial Ec is a common multiple of the CRC of this new CRC and CAN, it is still possible to construct an example of missed detection and calculate the new condition. Missing error detection frame probability. For example, the 8-bit DARC-8 generation polynomial x8+x5+x4+x3+1 does not contain the x+1 factor, so the error-error polynomial Ec composed of the least common multiple of the CAN generator polynomial will have 24 orders. As analyzed in Section 2.5, the total number of frames will increase by 28 times, while the number of missed frames will be the same, and the missed detection rate will be reduced by 28. However, the shortcoming of this method is that automatic error reporting cannot be implemented, and data consistency between nodes cannot be obtained. Nodes with local errors can not find errors after receiving the above measures, and it is impossible for other nodes to discard the frame. And require automatic retransmission. This paper proposes to use the 7b/8b encoding method, sacrificing some bandwidth, in exchange for the avoidance of mis-frame miss detection. The specific method is to select the part that does not have the padding condition in the 8b code for the original 7b encoding. Other coding methods are also feasible. Similar to 7b/8b, there are 6b/7b, 5b/6b, and 4b/5b. The difference between them is the complexity of software implementation and the amount of data occupied by overhead. When using 7b/8b CAN can send 7 bytes of data per frame, while 4b/5b can only send 6 bytes of data per frame. After the software patch of the additional data domain, if the padding rules in the ID field and the CRC field are only unilaterally executed, the control field sandwiched between them will move left or right, and the frame length will become larger or Become smaller. The unit of the frame length is 1 byte, which moves the CRC field into the EOF field. The CRC is the same for up to 5 consecutive bits, which destroys the EOF format, or the EOF field moves into the CRC field. The consecutive 8 bits of the EOF destroy the CRC padding format. So, the consequences of the unilateral execution of the padding rule at this time can be found. That is to say, after adding the software patch, there is no possibility that the wrong frame will be missed. If the suspicious Tx only occurs in the ID field, since Tx has a shortest length, corresponding to Ec, t= x3+x+1, this length is 3+15+6=24 bits, so the 29-bit ID for CAN2.0B may There will be an error, and the consequence is that the ID received by the receiving node is wrong. This is a kind of fake (Masquerade). In the reference [6], the CAN method for preventing falsehood is mentioned. In fact, the ID is divided into two parts, and one part is an additional CRC. As long as the CRC generation polynomial is different from CAN, no fake ID will be generated by receiving. The possibility of filtering. 4 Summary The error rate of CAN error frame has a great influence on the reliability of the application. This paper finds a method of suspicious frame reconstruction that may be missed. Therefore, the error rate of the wrong frame is higher than that provided by Bosch. Magnitude. For a system with a large number of high reliability requirements already applied, it is forced to cope with the solution. In 2007, the CAN chip shipped 600 million in one year [7], which shows that the impact is wide. This paper proposes a method for adding intermediate software patches for 7b/8b encoding/decoding to data. After sacrificing part of the bandwidth and adding some complexity, this method fundamentally solves the interference of the filling rule on the CRC check, and returns the missed frame miss rate of CAN to the same level as the CRC test in the general communication protocol. The data domain sacrifices a bandwidth of 8 bits. This is nothing compared to the possible 16-bit stuffing bits, and it reduces the jitter of the delivery time. It can be said that it is beneficial. The downside is the time and space required for encoding/decoding. This method can also be added to the chip in the future, using the reserved bits of CAN to identify the 7b/8b encoding/decoding function, thus achieving compatibility with the original CAN2.0. With the 7b/8b encoding/decoding function, the required 7b/8b encoding/decoding, word length rounding, and frame length correction can be done automatically by hardware.
008615081129555 south africa candles market is very big market .and 68g 65g 58g candles 6x25 packing are popular .
the white color candles made of 100% paraffin wax ,color is pure white .very strong .we aslo supply color candles .red yellow green blue .black color candles .you can choose .
welcome to visit my factory .
any candles inquire pls be free to contact with Me /ANGEL
South Africa Market Candle,South Africa Fluted Candle,South Africa White Candle,Africa Stick Fluted Candle Shijiazhuang Zhongya Candle Co,. Ltd. , https://www.zycandlefactory.com



![]()