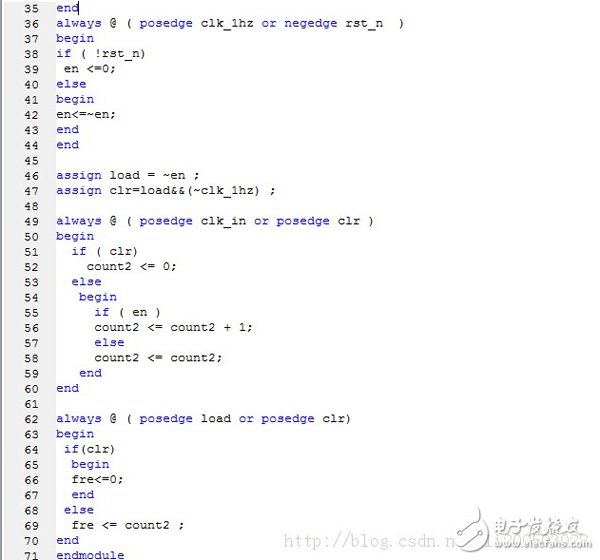
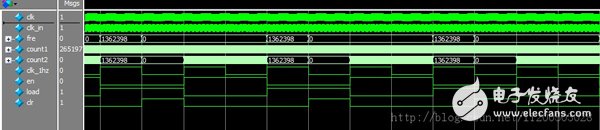
CORDIC is a set of algorithms that perform specific functions without a dedicated multiplier (minimizing the number of gates), including square, override, log, sin/cos/artan. The principle is to continuously rotate a small angle to approximate the desired angle with a certain precision. The specific principle is shown in the following figure: X_in[18:0], the unsigned integer to be squared, the input valid signal in nd(new data), the output x_out[9:0] and the corresponding enable signal rdy, the corresponding waveform diagram is shown in the following figure. (1) Flow delay At the bottom is the input data, and at the top is the output squared result. As can be seen from the above figure, from nd to rdy, there are 5 clock cycles. (2) Clock frequency The integrated clock frequency on the FX130-1 chip results in 2.8ns. When customizing the square root IP core, select Unsigned FracTIon and set X_IN and X_OUT to the same bit, 19 bits. Taking a project as an example, the square data needs to be represented by 19 bits. In the project, because the data to be opened represents the image coordinates, it is an integer, and the data format is UFIX19_0, that is, the data is represented by 19 bits, and the decimal place is zero. The input requirement of CORDIX is UFIX19_18, which is 19-bit data, of which 18 bits represent decimal places and 1 bit integers. In the case where the data format is inconsistent with the input of the CORDIC core, the bit of the output result needs to be correctly interpreted. Enter x_in=180: 000 0000 0000 1011 0100 Output x_dout=6869 1101 0101 Explanation: Because CORDIC expects the input x_in to be an 18-bit fraction, the CORDIC output x_dout should be a 9-bit fraction, ie 13+0.25+0.125+0.03125+0.0078125+0.001953125= 13.416. It can be seen that the minimum precision can be maintained to the third decimal place. In the specific implementation, it can be adjusted according to the accuracy requirements. Note: In fact, for the data format of 19 bits, 18bit decimal places and 1 bit decimal places represented by x_in, x_dout can be correctly interpreted without considering the shift; in other formats, x_dout needs to be correspondingly Shift interpretation, such as the above example, is a 9-bit right shift on x_dout to get the correct estimate. Vecsel Gain Chip,Laser Gain Chip,Laser Diode On A Chip ,Laser Diode Junction AcePhotonics Co.,Ltd. , https://www.cgphotonics.com
1. CORDIC function and principle