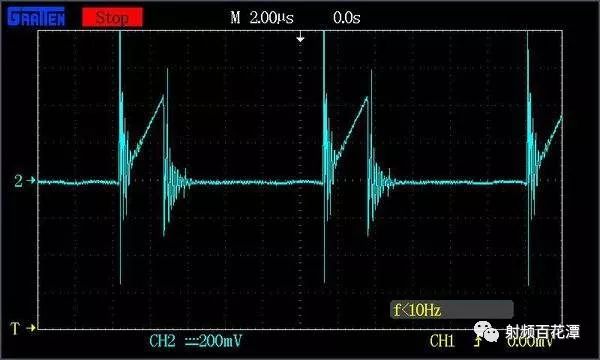
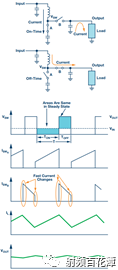
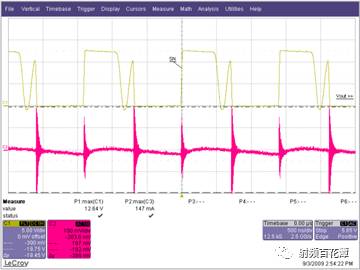
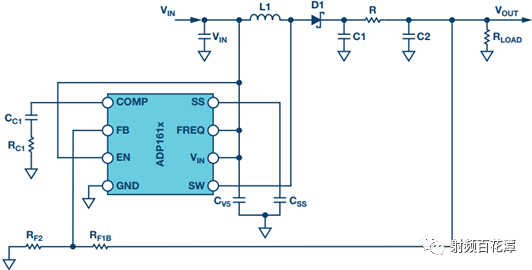
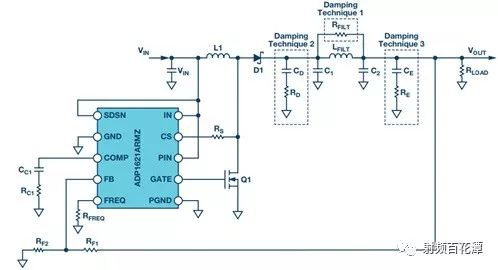
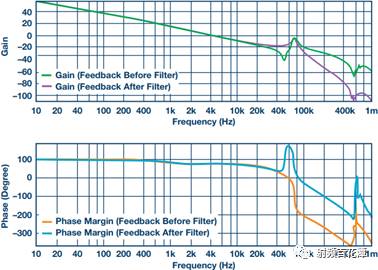
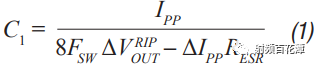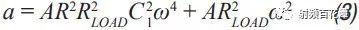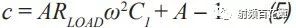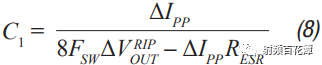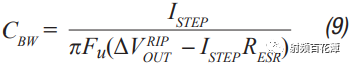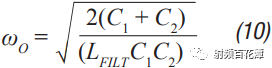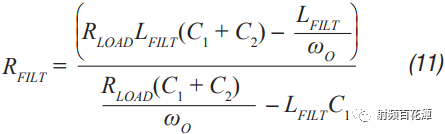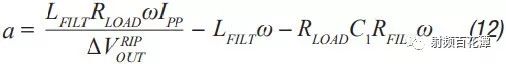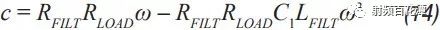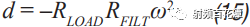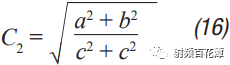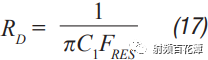Switching power supplies are used in almost all electronic devices. They are extremely valuable due to their small size, low cost and high efficiency. However, their biggest drawback is that high switching transients result in high output noise. This shortcoming makes them unusable in high-performance analog circuits that are powered by linear regulators. Practice has shown that in many applications, properly filtered switching converters can replace linear regulators to produce low noise power supplies. Even in demanding applications where very low noise power supplies are required, switching circuits may be present somewhere in the upstream power tree. Therefore, it is necessary to design a multi-stage filter that is optimized and damped to eliminate the output noise of the switching power converter. In addition, it is important to understand how the filter design affects the compensation of the switching power converter. The example circuit in this article will use a boost converter, but the results can be directly applied to any DC-DC converter. Figure 1 shows the basic waveform of the boost converter in constant current mode (CCM). Figure 1. Basic voltage and current waveforms of the boost converter The output filter is important for the boost topology or any other topology with a discontinuous current mode because it has a fast rise and fall time in switch B. This can result in parasitic inductance in the excitation switch, layout, and output capacitors. As a result, in actual use, the output waveform looks more like Figure 2 rather than Figure 1, even if the layout is good and ceramic output capacitors are used. Figure 2. Typical measurement waveform of a boost converter in DCM The switching ripple (switching frequency) due to the change in capacitance charge is very small compared to the undamped ringing of the output switch, hereinafter referred to as output noise. In general, this output noise ranges from 10 MHz to over 100 MHz, well beyond the self-resonant frequency of most ceramic output capacitors. Therefore, adding additional capacitance has little effect on noise attenuation. There are also many types of filters suitable for filtering this output. This article will explain each filter and give each step of the design. The formulas in the paper are not rigorous, and some reasonable assumptions have been made to simplify these formulas to some extent. Some iterations are still needed because each component affects the values ​​of other components. The ADIsimPower design tool avoids this problem by using a linearization formula of component values ​​(such as cost or size) to optimize the components before actually selecting them, then selecting the actual components from a database of thousands of devices and optimizing their output. . But at the beginning of the design, this level of complexity is not necessary. With the calculation formula provided, using a SIMPLIS simulator – such as the free ADIsimPETM – or spending some time on the lab bench, you can get a satisfactory design with minimal effort. Before you start designing the filter, consider what a single-stage filter RC or LC filter can do. A secondary filter is typically used to properly reject ripple to a few hundred μV pp and to suppress switching noise below 1 mV pp. The buck converter is less noisy because the power supply inductance provides good filtering capability. These limitations are due to the fact that once the ripple is reduced to the μV level, the noise coupling between the component parasitics and the filter stage begins to become a limiting factor. If a less noisy power supply is used, a three-stage filter is required. However, the reference voltage source for a switching power supply is generally not the lowest noise component and is often affected by jitter noise. These all result in low frequency noise (1 Hz to 100 kHz) and are usually not easily filtered out. Therefore, for very low noise power supplies, it may be more appropriate to use a single secondary filter and then add an LDO at the output. Before describing the design steps of each type of filter in more detail, some of the values ​​of the various types of filters used in the design steps are defined as follows: ΔIPP: Approximate peak-to-peak current into the output filter. For the convenience of calculation, it is assumed to be a sinusoidal signal. The value depends on the topology. For a buck converter, it is the peak-to-peak current in the inductor. For a boost converter, it is the peak current in switch B (usually a diode). ΔVRIPOUT : Approximate output voltage ripple at the converter switching frequency. RESR: ESR of the selected output capacitor. FSW : Converter switching frequency. CRIP: In the calculation of the output capacitance, it is assumed that all ΔIPP flows into it. ΔVTRANOUT: The change in VOUT when ISTEP is applied to the output. ISTEP: Instantaneous change in output load. TSTEP: Approximate response time of the converter for instantaneous changes in output load. Fu: The crossover frequency of the converter. For buck converters, the value is usually FSW â„10. For a boost or buck/boost converter, it is typically located at approximately 1/3 of the right half plane zero (RHPZ). The simplest type of filter is the RC filter, as shown in Figure 3 based on the output of the low current ADP161x boost design. This filter has the advantage of low cost without the need for damping. However, due to power consumption, it is only useful for very low output current converters. This article assumes that ceramic capacitors have a lower ESR. Figure 3. ADP161x Low Output Current Boost Converter Design with RC Filter Adding to the Output RC secondary output filter design steps Step 1: C1 is selected according to the following conditions: assuming that the output ripple approximation of C1 can ignore the remaining filters; 5 mV pp to 20 mV pp is a good choice. C1 can then be calculated by Equation 1. Step 2: R can be selected based on power consumption. R must be much larger than RESR, and the capacitor and this filter will work. This limits the range of output current to less than 50 mA. Step 3: C2 can then be calculated using Equation 2 through Equation 6. A, a, b, and c are intermediate values ​​for simplified calculations and have no practical significance. These formulas assume R < LOAD and the ESR of each capacitor is small. These are good assumptions and the introduced errors are small. C2 should be equal to or greater than C1. The ripple in step 1 can be adjusted to make it possible. For higher current sources, it is advantageous to replace the resistors in the pi filter with the inductors in Figure 4. This configuration provides excellent ripple and switching noise rejection with low power consumption. The problem is that we are now introducing an additional tank circuit that can create resonance. This can cause oscillations and make the power supply unstable. Therefore, the first step in designing the filter is how to choose the damper filter. Figure 4 shows three possible damping techniques. Adding RFILT has the advantage of additional cost and less size increase. Damping resistors typically have little or no loss, even in the case of large power supplies. The disadvantage is that it reduces the parallel impedance of the inductor, which greatly reduces the effectiveness of the filter. The second technique has the advantage of maximizing filter performance. If an all-ceramic design is required, the RD can be a discrete resistor in series with the ceramic capacitor. Otherwise use a capacitor with a high ESR and a large physical size. This extra capacitance (CD) will significantly increase the cost and size of the design. Damping Technology 3 appears to be a great advantage because the damping capacitor CE is added to the output, which may be beneficial for transient response and output ripple performance. However, this technique is the most expensive because of the large amount of capacitance required. In addition, the relatively large number of capacitors at the output reduces the resonant frequency of the filter, which in turn reduces the bandwidth that the converter can achieve – so the third technique is not recommended. For the ADIsimPower design tool, we use the first technique because it is less expensive and relatively easy to implement in automated design steps. Figure 4. ADP1621 with output filters and highlighting many different damping techniques Another issue to be aware of is compensation. Although this may not be intuitive, it is almost always better to put the filter inside the feedback loop. This is because placing it in the feedback loop helps to suppress the filter to some extent, eliminating the DC load offset and the series resistance of the filter, while providing better transient response and lower ringing. . Figure 5 shows a Bode plot of a boost converter with an LC filter output added to the output. Figure 5. Boost converter with LC filter at the output The feedback is taken before or after the filter inductance. What people didn't expect was that even if the filter was not inside the feedback loop, the open-loop Bode plot still had a very large change. Since the control loop is affected regardless of whether the filter is in the feedback loop, it should be properly compensated. In general, this means that the target crossover frequency is adjusted downwards to no more than one-fifth to one-tenth of the filter resonance frequency (FRES). The design steps of such filters are essentially an iterative process because the choice of each component affects the choice of other components. LC filter design step using parallel damping resistor (first technique in Figure 4) Step 1: Select C1 to make it equal to when the output has no output filter. 5 mV to 20 mV pp is a good start. C1 can then be calculated by Equation 8. Step 2: Select the inductor LFILT. Based on experience, the preferred range is from 0.5 μF to 2.2 μF. The inductor should be selected in accordance with the high self-resonant frequency (SRF). Larger inductors have larger SRFs, which means their high frequency noise filtering efficiency is poor. Smaller inductors have less impact on ripple and require more capacitance. The higher the switching frequency, the smaller the inductance value. When comparing two inductors with the same inductance value, devices with higher SRF have lower inter-winding capacitance. The inter-winding capacitance acts as a short circuit around the filter and acts on high frequency noise. Step 3: As mentioned earlier, adding a filter affects converter compensation by reducing the achievable crossover frequency (Fu). According to the calculation of Equation 7, the maximum achiviable achievable for current mode switching is 1/10 or less of the switching frequency, or 1/5 or less of the filter FRES. Fortunately, most analog loads do not require too much transient response. Equation 9 calculates the approximate output capacitance (CBW) required for the converter output to provide the specified transient current step. Step 4: Set C2 to the minimum of CBW and C1. Step 5: Calculate the damper filter resistance approximation using Equation 10 and Equation 11. These formulas are not absolutely accurate, but they are the closest closed solution that does not use pan-algebras. The ADIsimPower design tool calculates the RFILT by calculating the open-loop transfer function (OLTF) of the converter when the filter and inductor are shorted. The RFILT value is the guess value until the filter is only the peak of the converter OLTF (inductor short circuit) at 10 dB above the converter OLTF. This technique can be used in simulators such as ADIsimPE or in laboratories using spectrum analyzers. Step 6: C2 can now be calculated using Equation 12 through Equation 15. a, b, c, and d are used to simplify Equation 16. Step 7: Steps 3 through 5 should be repeated until an excellent damper filter design that meets the desired ripple and transient specifications is calculated. It should be noted that these equations ignore the DC series resistance RDCR of the filter inductor. This resistance can be very large for lower supply currents. It improves filter performance by helping to suppress the filter, increasing the required RFILT while also increasing the filter impedance. Both of these effects greatly improve filter performance. Therefore, it is cost-effective to exchange low power consumption in LFILT for low noise performance, which can improve noise performance. The core loss in LFILT also helps to attenuate some of the high frequency noise. Therefore, a high current powered ferromagnetic core is a good choice. They are smaller and less expensive with the same current capability. Of course, ADIsimPower has the filter inductor resistance value and the ESR value of the two capacitors for the highest accuracy. Step 8: When selecting the actual components to match the calculated values, be careful to reduce the rating of any ceramic capacitors in order to take DC bias into account! As mentioned earlier, Figure 4 shows two possible techniques for suppressing filters. If the shunt resistor is not selected, the CD can be selected to suppress the filter. This adds some cost, but it provides the best filter performance compared to any other technology. LC filter design step using RC damping network (2nd technique in Figure 4) Step 1: As in the previous topology, select C1 to make it equal to when there is no output filter. 10 mV pp to 100 mV pp is a good start, depending on the final target output ripple. C1 can then be calculated by Equation 8. C1 can use smaller values ​​in this topology than previous topologies because the filters are more efficient. Step 2: In the previous topology, select an inductor with a value from 0.5 μH to 2.2 μH. 1 μH is a good value for converters from 500 kHz to 1200 kHz. Step 3: As before, C2 can be selected from Equation 16, but RFILT should be set to a larger value, such as 1 MΩ, because the component will not be installed. Regardless of whether C1 has additional capacitance, the reason for its constant value is that in order to provide good damping, the RD will be large enough that the CD does not reduce the ripple too much. Set C2 to the minimum value calculated by C2, CBW, and C1. It is useful to go back to step 1 and adjust the ripple on C1 so that the calculated C2 is approximately equal to CBW and C1. Step 4: The value of CD should be equal to C1. In theory, more suppression of the filter can be achieved with a larger capacitor, but it unnecessarily increases cost and size and reduces converter bandwidth. Step 5: RD can be calculated by Equation 17. FRES is calculated by Equation 7, ignoring the CD. This is a good approximation because Rd is usually large enough that the CD hardly affects the filter resonance position. Step 6: Now, both CD and RD have been calculated. Ceramic capacitors with series resistors can be used, or tantalum or similar capacitors with large ESR can be selected to meet the calculated specifications. Step 7: When selecting the actual components to match the calculated values, be careful to reduce the rating of any ceramic capacitors in order to take DC bias into consideration! Another filter technique is to replace the L in the previous filter with a ferrite bead. However, this approach has a number of disadvantages that limit the effectiveness of switching noise filtering and have little benefit to switching ripple. The first is saturation. The ferrite bead will saturate at very low bias current levels, which means that the ferrite will be much lower than the zero bias curve shown in all data sheets. It may still need to be suppressed because it is still an inductor and therefore will follow the output inductor resonance. But now the inductor is a variable and is very poorly characterized by the very small amount of data that most data sheets can provide. For this reason, ferrite beads are not recommended as secondary filters, but can be used downstream to further reduce extremely high frequency noise. in conclusion This article provides a variety of switching power supply output filter technology. This article provides a step-by-step design process for each topology, reducing guess time and reducing checks in filter design. The formulas in this paper have been simplified to some extent, and engineers can achieve rapid design by knowing the extent to which the secondary output filter can be achieved.
·Basic precautions
Do not put expensive oil into low-quality cartridges to avoid wastage. Most pre-filled oil cartridges have the so-called 510 thread. The oil cartridge screws onto a rechargeable battery. Some of these batteries have buttons and some heat up automatically when you pump the oil. Some batteries have multiple temperature settings and some heat up to a preset temperature; these features need to be known in advance.
·Cleaning notes
Use a suitable cleaning tool to clean them, such as activated charcoal or dried tea leaves in a used pipe to absorb the oil. It is important not to use alcohol or other boiling water to clean the pipe, and to wait until it has cooled down completely before cleaning. Otherwise, the hot stem will come into contact with the watery liquid and cause the mouthpiece tenon to loosen, thus shortening the life of the 510 cartridges.
This is what you should be aware of when using 510 cartridges. At the same time, when using 510 cartridges, there are still some vaping tips, for example, when using them, be careful not to suck too hard, will not produce smoke. When you inhale too hard, the smoke is sucked directly into your mouth and not atomized by the atomizer, so gently inhaling is more powerful and gives you a better vaping experience.
510 Cartridge Oem,Leakproof 510 Cartridge,510 Battery And Cartridges Oem,510 Cartridge Shenzhen MASON VAP Technology Co., Ltd. , https://www.masonvap.com