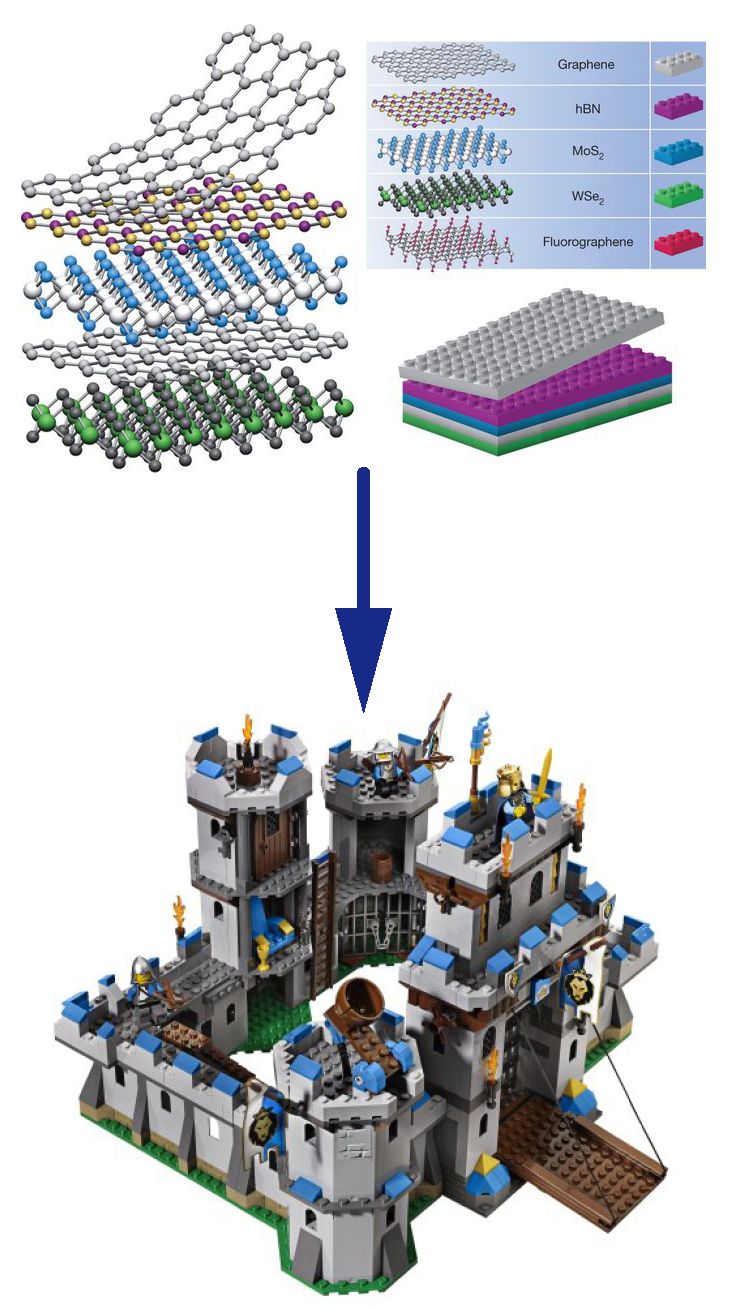
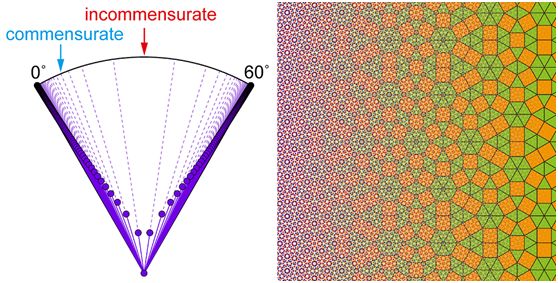
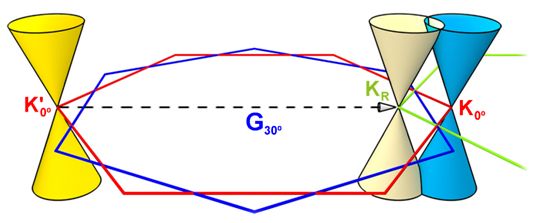
The two-dimensional material system represented by graphene has attracted the attention of researchers due to its rich electrical, optical, mechanical and other characteristics and wide application prospects. By stacking different two-dimensional materials to form a van der Waals heterojunction, the properties of these two-dimensional materials can be further adjusted to achieve new properties not possessed by a single material. Double-layer graphene can be regarded as the simplest van der Waals "hetero" junction. Through the twist angle between the two graphene layers, band regulation and novel physical properties can be achieved. In the torsion angle double-layer graphene system, most of the current research work is mainly focused on the double-layer graphene with a long-range periodic commensurate structure, while for the incommensurate structure formed by large torsion angles The research on the double-layer graphene is rarely involved. The research team led by Zhou Shuyun from the Department of Physics of Tsinghua University selected a quasicrystalline bilayer graphene formed at a 30 ° twist angle as a typical representative with an uncommon structure. The unique mirror Dirac cone was observed in the electronic structure, revealing A more general new mechanism describing the coupling between layers. This result was published in the recent "Proceedings of the American Academy of Sciences" [1]. The corresponding author of the article is Professor Zhou Shuyun from Tsinghua University and Professor Zhu Junyi from the Chinese University of Hong Kong. The first author is Yao Wei from the Zhou Shuyun research group. This article gives a brief introduction to this quasicrystalline bilayer graphene research work. Graphene's historical mission As the process technology of modern silicon-based semiconductor chips approaches the quantum limit, Moore's Law, which has been proposed for more than half a century, is also gradually coming to an end. Of course, human beings will not stop here. On the one hand, people are trying to improve the basic structure of transistors in current large-scale integrated circuits. On the other hand, they are looking for a new type with better performance that is expected to replace monocrystalline silicon. Materials, under this goal, a two-dimensional material revolution represented by graphene is quietly unfolding. In 2004, Geim and Novoselov of the University of Manchester successfully prepared graphene samples on a silica substrate using the classic "tearing tape" method, that is, single-layer graphite with atomic thickness [2]. Once discovered, this material with a hexagonal honeycomb structure (Figure 1) exhibits unusual mechanical, thermal, and electrical properties. Relying on its unique Dirac cone linear performance band structure, graphene has an ultra-high electron mobility, which makes it one of the hottest candidate materials for manufacturing electronic chips in the future, and Geim and Novoselov are also honored. 2010 Nobel Prize in Physics [3]. Figure 1. Graphene More is different: Stacking and twisting With the birth of graphene, this type of two-dimensional material system with a layered structure provides a vast world for physics and materials scientists to explore novel physical states and physical properties. In the past ten years, a large number of distinctive two-dimensional materials have emerged endlessly. The most representative ones include transition metal disulfides, black phosphorus, hexagonal boron nitride, and bismuth, selenium and tellurium families. These materials include almost all of the major solid states known to man, including metals, semiconductors, ordinary insulators, topological insulators, superconductors, and charge density waves. They also expand some new intrinsic degrees of freedom that can be controlled by electro-optics, such as Energy group pseudo spin in monolayer of transition metal disulfide, etc. Although every two-dimensional material has interesting enough properties, experimental physicists are not satisfied with it, as PW Anderson, a condensed matter physics master, said: More is different, more is different. In their eyes, the two-dimensional material world is a Lego kingdom. Each two-dimensional material is like a building block. Through reasonable assembly combinations, they can explore and control more wonderful physical characteristics and build a more magnificent castle. (figure 2). So people put forward the idea of ​​constructing the so-called van der Waals heterojunction [4], that is, by stacking different types of two-dimensional thin film materials, using the van der Waals force between the layers as the connection glue, a special heterogeneity is formed structure. What people expect is that the interlayer coupling inside the heterojunction can induce properties different from when the components of the heterojunction exist independently. At this step, experimental physicists have made very important progress. For example, when combining a single layer of graphene with a single layer of hexagonal boron nitride, the interaction between the layers will lead to the so-called second set of Di Lack point, this is a property that single-layer graphene does not have [5,6]. Figure 2. The castle of the two-dimensional material world. The above picture is from [4] In fact, if the "heterogeneity" condition in the heterojunction is relaxed, the effect of interlayer coupling will become more obvious, and graphene once again acts as our Lego building block (Figure 3). It is well known that large-scale integrated circuits are composed of many transistors, that is, controllable logic switching elements. Although single-layer graphene has a strong advantage in electrical conductivity, its band gap-free energy band structure So that it can not easily realize the logic switch function. One possible solution is to use two layers of graphene stacked from two layers of graphene. Double-layer graphene itself is a conductor without energy gap. However, once an electric field is added to the outside world, the energy gap will be effectively opened [7], which can isolate the conduction of electrons and realize a prototype logic switch. This shows that even in the simplest "heterogeneity" junction of double-layer graphene, there are great possibilities for realizing future electronic chips. Figure 3. Van der Waals heterojunction: stacking of two-dimensional materials So can there be more changes and differences? The answer is yes. A seemingly simple but not mediocre idea is to rotate the two layers of two-dimensional material in the heterojunction to form a certain torsion angle (Figure 4). Let us once again come to the simple and magical example of double graphene. Double-layer graphene generally refers to an AB stack or an AA stack formed by overlapping the crystal axes of two layers of graphene, wherein the AB stack can generate the aforementioned energy gap. When we introduce the additional degree of freedom of rotation angle, both the lattice structure and the electronic structure will have more abundant changes. First of all, from the crystal structure point of view, when the two layers of graphene are twisted, the structure will be divided into common and non-common degrees. In the common structure (generally appearing under small torsion angles), the double-layer graphene will form so-called Moiré stripes, and the whole still has long-range periodicity. From the point of view of the electronic structure, the theory predicts that in some common twisted graphene with special twist angles (called "magic angles"), some flat band structures will appear in the energy bands of the system, that is, energy bands without dispersion . Experimentally, the twisted double-layer graphene with "magic angle" has been proved to have the ground state of the Mott insulator phase [8], and after proper electron doping, it can further realize the superconducting state [9]. The strong correlation of electrons in such a pure carbon-based system undoubtedly surprises and excites all workers in the field of condensed matter physics, and also fully shows the infinite potential of the double-layer graphene system. The difference from the metric structure is that in non-metric structures (generally appearing under large torsion angles), this long-range periodicity will no longer exist, and even "quasicrystals" will form at some special torsion angles. It is difficult to describe with traditional solid physical theory. Figure 4. New degrees of freedom: twist angle For a long time in the past, the theoretical and experimental work on torsion angle double-layer graphene has mainly focused on the double-layer graphene that easily forms a common structure in a small angle range. However, the research on double-angle torsion graphene with non-common degree structure is extremely rare. On the one hand, there are few naturally-formed non-common degree double-layer graphene. On the other hand, it is generally believed that non-common degree is easy to form Under the condition of large torsion angle of the structure, the interlayer coupling of the torsion angle double-layer graphene will be sharply weakened, thus lacking interesting physics. A recent report from the Academy of Sciences of the United States of America reported the results from the research team of Zhou Shuyun of Tsinghua University. The team successfully prepared a double-layer graphene with a twist angle of 30 ° and gave a novel Dirac cone and energy band coupling caused by the structure. Related physical mechanisms [1]. Mirror Dirac cone in quasicrystalline bilayer graphene For the van der Waals heterojunction, the formation of a molar periodic potential closely related to lattice matching has a great influence on the interaction between layers. If there is a molar periodic potential, then the interlayer coupling will be enhanced due to phase coherence, and vice versa. In twisted-angle bilayer graphene, torsion angle is the only factor that determines whether the molar cycle potential can be formed. It can be known from mathematical calculations that in a 60 ° torsion cycle, the torsion angles that can form a lattice match to produce a molar periodic potential are mainly concentrated around 0 ° or the equivalent 60 ° torsion angle (Figure 5 left), and Near the 30 ° twist angle, almost no angle can form a molar periodic potential, especially the special degree of 30 °. Under this torsion angle, the double-layer graphene shows a class of twelve-fold symmetric quasi-crystalline stripes (Figure 5 Right), indicating that the corresponding torsion angle bilayer graphene does not form long-range periodicity. Figure 5. Left: Correspondence between metric or non-metric structure and torsion angle. Right: Quasicrystal stripes in a double-layer graphene with a 30 ° torsion angle. According to the traditional concept, the energy band structure of the non-common degree twisted double-layer graphene is simply the superposition of the energy band structures of the two single-layer graphene, as 1 + 1 = 2. But the researchers found that this is not the case, 1 + 1 ≠2. For the first time, Zhou Shuyun's research group successfully grown a double-layer graphene with a 30 ° twist angle on a metal Pt (111) substrate, and directly measured the clear energy band structure of the system using angle-resolved photoelectron spectroscopy (ARPES) experimental technology. They found that in addition to the linear performance bands from the two layers of graphene, that is, the Dirac cone, within the Brillouin zone of graphene, a series of additional Dirac cones appeared. They and the original Dirac cone The mirror symmetry is formed, and their symmetric mirrors are unbiased, which happens to be the boundary of the Brillouin zone of another layer of graphene (Figure 6). This result shows that the appearance of specular Dirac cone is not accidental, but comes from the intrinsic electronic structure of the double-layer graphene with a 30 ° twist angle. Among them, the interlayer coupling between the two layers of graphene is indispensable. Figure 6. The generation mechanism of mirrored Dirac cone in double-layer graphene with 30 ° twist angle The researchers further analyzed the mechanism of the appearance of the mirrored Dirac cone. They found that if the original Dirac cone dual to the mirrored Dirac cone is at the point K, then the mirrored Dirac cone is actually caused by another at the K 'point, That is, the original Dirac cone at the opposite of the K-point momentum is scattered (Figure 6). This scattering momentum is exactly an inverted lattice vector (G30 °) of the bottom graphene, which means that the electrons in the top graphene feel the bottom graphite The role of olefin lattice field. In the Raman spectroscopy analysis of this study, the double resonance Raman mode observed by the researchers also strongly supports such a mechanism. What general physical law is the underlying magic mirror layer superimposed on the two graphenes above that could not be superimposed on the electronic states K and K '? The theoretical and computational team from the Department of Physics of the Chinese University of Hong Kong conducted detailed analysis and computational research on this naturally occurring magic mirror structure. They derived the universal condition that the two wave vectors of the upper graphene can be scattered by the lower mirror layer and the superimposed condition is that the difference between the two wave vectors of the upper layer is exactly equal to the difference of the inverted lattice vectors of the upper and lower layers. This rule applies not only to graphene, but to any two-dimensional material stack. It is also under the action of this mechanism that the graphene layer and the platinum substrate produce a sufficiently large pd orbital coupling effect, so that the magic mirror graphene can naturally occur during crystal growth. This mechanism is completely different from the coupling mechanism of the conventional low-angle graphene produced by artificial stacking. We can think of the two electronic states of the K and K 'points of single-layer graphene as the never-seeing stars and quotients in this graphene small world. Then, a miracle appeared, one with this graphene world has three The ten-degree corner "corner universe" graphene is like a magic mirror, allowing two stars that never meet to be superimposed under the scattering of the magic mirror, shining brightly. In a kind of poetic fantasy, maybe there is such a corner world outside our world. Although we do n’t seem to feel its existence, as long as this scattering condition is met, it can produce miracles, so that we can never meet. The electronic states meet each other, and our world is also the magic mirror of that magic mirror world. The experimental realization of quasi-crystalline graphene provides an important carrier for the mirror Dirac cone. This mechanism and the experimental results behind it abandon the dependence on the molar periodic potential in the past heterojunction research, and provide a new perspective for describing the interaction between heterojunction layers. On the other hand, the research results use a 30 ° twisted double-layer graphene as a simple model, and the "magic mirror" effect it finds can be used to regulate more and more complex electronic structures in the van der Waals heterojunction in the future. Open up new paths. Custom Co-Based Amorphous Ribbon,New Type Nano Ribbon,Good Fe-Based Amorphous Ribbon,New Type Co-Based Ribbon Anyang Kayo Amorphous Technology Co.,Ltd. , https://www.kayoamotech.com